Discrete Mathematics and Probability Theory
Wooooooo! That was Professor Rao’s way of waking up the entire class for the 8 AM Zoom lecture. Coincidentally it would also be the one word I use to describe my experience taking this class. Oh my was this class a delight to take. The main reason why was because I elected to take this class pass no pass. The pressure was off to get that A. Additionally, my housemate and I were both enrolled in this course, and the late-night last-minute homework cramming sessions will likely last as a pleasant memory of my remote semester. Finally, the curriculum of CS 70 was too good to be true for me. I will explain later.

Early chapters covered basic boolean algebra 
Modular arithmetic 
Intro to graph theory via the classic Konigsberg Bridge Problem
Firstly, it is always a treat when I am able to take a course pass-no-pass. CS 70 is not a required course for me, but is a recommended prerequisite for CS 189, which is Berkeley’s well-reputed course introducing Machine Learning. Due to my intent on taking CS 189, I decided to throw in CS 70 to my schedule. PNP allows me both to learn the material and also not stress over those elusive As in the formidable CS department. Without the pressure to perform at a top level, I was learning purely out of interest. When such is the case, learning becomes 100% enjoyable and 0% tedious in contrast to some combination of both for classes I take for grade.
Secondly, as a result of my lack of motivation to complete homework (perhaps encouraged by my decision to take the class PNP) as well as my housemate’s similar work style, we often found ourselves in a predicament on Friday nights, struggling to meet that 10 PM deadline for our weekly homework set. He would have watched lecture and read notes, I would have done neither, and we would muscle our way through the 6-problem set. My adrenaline rush would force me to learn while I worked. I was skimming through notes at lightning speed while my housemate and I discussed and disagreed on solutions, trying desperately to make each other understand our own perspectives all the while alternative rock blasts on my Amazon Echo. Push comes to shove and we end up just saying “f*ck it” and submitting whatever we had while praying to the discrete deities. This style of run-and-gun learning and assignment completing, though far from the most effective, is certainly the most exciting. This was an excitement I had not felt in a while and became my lame version of “turning up on a Friday” during quarantine.
Finally, the curriculum of CS 70 is my style. Whether we were learning about graph theory, stable marriage, or probability theory, one aspect remained the same: the problems required ingenuity. I am not saying I am a genius, I am far from it, but that is not to say I cannot enjoy a brain-teaser. Each example, each problem, each proof, could not be solved by simple regurgitation of fact and formula combined with computation. Each one required a stroke of creativity, a flash of brilliance. Afterwards, there was surprisingly little busy-work involved. This is the style of curriculum I love. It is certainly not easy and can take infuriatingly long hours to grapple with, but it is all in good fun for me. Coupled with my decision to PNP, I did not mind this course at all.
Ultimately this course was like an enjoyable roller coaster. Now reader beware, the class is NOT typically considered a joyride and can be quite, if not extremely stressful and difficult if you are aiming for perfection. I, however, had little pressure to study (or not study :P) a subject I liked. Heck that is uncannily similar to the definition of a “hobby”.
Food For Thought
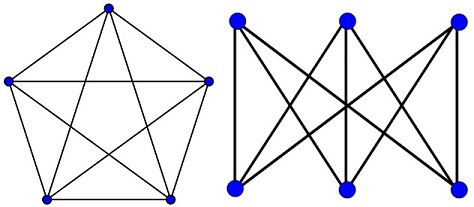
The following two graphs are known as the K5 and K33 graphs respectively. They are famously non-planar. How many edges minimum need to be removed from each to make them planar? (Hint: the two form a basis for all other non-planar graphs).