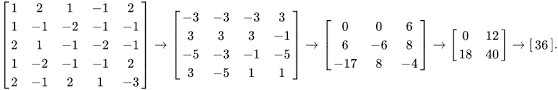Math 54

Ah, linear algebra, the course that abstractifies what a dimension is and opens the gateway into infinite possible “other dimensions”.  This course is a true paradigm shift in how to understand a mathematical topic previously misunderstood to be basic when I was in 7th grade.  Such was indeed my first impression of this class: “didn’t I learn this already 7 years ago?”.  Turns out the answer was yes and no.  I learned a tiny subset of linear algebra.  This class offered the sample space, and my God is it huge.  

I will not go into the details of what this class covered, as it is a fairly standard class taught at almost every university and even some high schools that almost all STEM majors will be required to take eventually.  For this reason, I assume the curriculum is well established and does not need to be re-explained by a questionably qualified undergraduate.  Instead, I will recount my personal experience and feelings towards the subject matter.  

As with many abstract academic disciplines (eg. Math, Physics, CS theory), I am always fascinated by their ability to continuously amaze me while simultaneously reminding me how stupid I truly am despite all my years of education.  In high school, when I first learned calculus, I was opened up to the world of the infinitely small, and the infinitely large.  Much of what I knew about what “math” was changed that year.  Applying this knowledge to Physics courses changed what I knew about what “Physics” was.  Calculus-based derivations to previously plug-and-chug equations were elegant and again helped me redefine a subject matter.  

Linear Algebra is truly special because it doesn’t even necessarily try to introduce me to a topic I had never been exposed to.  It did not need to teach me something completely new to amaze me.  Instead, it seeks to take problems I have long been able to solve and generalize it to an entire universe of problems that seem vastly different at the outset but prove to be similar upon closer examination.  As a somewhat recursive analogy, I would consider the entire world of linearly-solvable problems to be of an arbitrarily large space V.  2-variable algebra which I learned in middle school provides me with a single vector in the basis of V.  With it, I am only able to solve a very specific subset of problems in V.  Math 54 provides me with an arsenal of remaining vectors that complete the basis set of V, thus allowing me to conquer ANY linearly-solvable problem. 

In conclusion, my experience with Math 54 was overwhelmingly positive.  I was fortunate to have a great professor, Prof Srivastava, who really dove deep into the core of the subject instead of providing surface-level problem-solving tools which only helped for the sake of completing homework sets.  Despite the difficulty, this course joins the list of courses that have redefined subjects for me.  And hey, even if I forget most of the topics down the road, at least I’ll always vaguely know what Tony Stark is talking about in Avengers Endgame when he says “eigenvector”.